week 1 - may 25th

I finally arrived in College Station, eager to be working on whatever it is that I am to be working on. As it turns out, I'm not certain of the exact project, but I do know that it will somehow involve the usage of STAPL, which is the parallel extension of C++'s STL that is being developed at Texas A&M. So in order to have an idea what the upcoming weeks will be like, I spent the majority of this week familiarizing myself with the basics of the STAPL framework.

A large undertaking indeed.

I started off by reading several papers on STAPL:

It was suggested that my research project should be focused in the field of motion planning. I was at a complete loss as to what that could even mean so I was given even more reading:

The rest of the week was spent playing around with STAPL and trying to get a feel for the major components: pContainers, pAlgorthims, and pRanges. I spent some time figuring out how to use SVN to update the source files, compile the source code, and mess with the test files to understand how the framework worked, in general. I eventually ended up writing a few (unoptimized) work functions that populated and searched generic STAPL containers. I became pretty familiar with work functions in general so hopefully this is a good sign for the weeks to come.

week 2 - june 1st

I started off the week messing around with STAPL and seeing how the parallelization process increases efficiency. I ran numerous tests with a work function of complexity O(n) and the results indicated that for large values of n, the parallized code's efficiency was directly propotional to how many CPUs were involved. For example, when I ran the function on an eight processor node, the time it took to execute was one-eigth of the time it takes to run on one CPU. This comes as no surprise.

I was given a brief overview of partial specialization with regard to how it is implemented in STAPL. This was mostly accomplished by reading Design for Interoperability in STAPL by the STAPL group here in the Parasol lab. The paper mostly dealt with using specialized linear algebra algorithms from an external library and seamlessly integrating them into the STAPL framework. I tried to work on some of the written code that used external matrix multiplcation code.

In order to view how these algorithms held on a large scale, I needed to test them on a IBM p575 cluster called hydra. Getting an account on hydra was a journey in and of itself. It took quite a while to get everything set up to the way it was supposed to be. Once it did (partially) work, I ran a few test files dealing with matrix multiplication on the pMatrix. I then tried to fully understand the code dealing with the pMatrix because this will be the area of my summer research.

Next week will be spent mostly on implementing the various matrix multipilcation specializations in STAPL.

week 3 - june 8th

This week was spent trying to incorporate many of the different cases for matrix-matrix multiplication into STAPL's pMatrix class. The provided code only worked for the very specialized case of row-major, column-major, row-major where the major signifies the physical distribution of the matrix's data. This case is actually the easiest case to implement, due to how the general matrix multiplication algorithm is laid out. Although I now have a deeper understanding of how the matrix class works, how the current multiplication function is supposed to behave, and STAPL's way of laying out data (views, containers, domains, etc.), I spent the majority of the week trying to make the algorithm work for other cases only to realize that it was not possible for any of the other cases to work with the way I was doing it. Which is unfortunate because this realization came only after many hours of compilation errors, random results, and segmentation faults.

So we as a group took a step back and with the help of our mentors, we decided that we should figure out how the algorithm should work on paper before we commit any more time to coding, which we should have done in the first place. We managed to come up with tentative solutions for 75% of the cases that we would encounter in normal usage. It was hypothesized by Gabi that the other cases might actually be impossible with the way STAPL currently does things and we should spend more time thinking about these cases.

So after all of that pen and paper work, we will spend next week working out some of the finer details, like offsets and memory management, and start converting these results into actual, usable code.

week 4 - june 15th

This week was spent mostly trying to implement the various cases that were worked out on paper for the previous week. We were able to implement two more cases in addition to the one that was already written before we started working on it. The implementation process is pretty straight forward and we were able to work at the pace of about one case every two days.

Not only did we spend the week coding, but we also ensured the validity of the results and the efficiency of the algorithm. The algorithm did indeed return the correct results if given the specific data arrangement, but the speed up compared to the original case was somewhat lacking. On average, our algorithm performed 14% slower than the provided one. We are currently looking to resolve this by obtaining more acceptable results through optimization before we attempt to integrate any more cases into STAPL.

So next week should be about optimization and then hopefully some more progress on the rest of the specializations.

week 5 - june 22nd

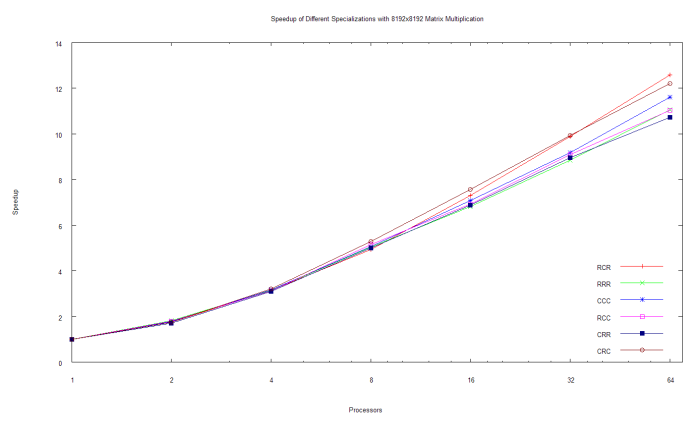
This week was actually very interesting. We finished up three more specializations for the matrix-multiplication algorithm and then ran several tests in batch to determine how our versions compared with the one that was provided. After a little testing and optimization, we saw that the several different algorithms did not differ greatly from each other and that the speedups were relatively similar. I've included an updated graph that illustrates how all of the algorithms look against one another. So after coding and testing six of the eight possible cases, we decided to seek advice on how to handle the last two cases.

a crappy graph for jerks

It turns out that the work we were doing was not actually the work that was intended for us to do. It kind of was and it kind of wasn't. What we should have been doing was taking the algorithm given to us (that is, multiplying a row of the first matrix with a column from the second matrix and storing the result one element at time) and applying it to the many different possibilities of traversal direction and storage layout. For example, if the first matrix is stored by row but the individual blocks are viewed by column, we would have to change the underlying multiply techniques (the call to BLAS needs to be modified with regard to the different flags being passed).

Making the changes expected of us should be significantly easier than the work we had been doing the past few weeks and I estimate that we can implement most of it by the end of next week. On the other hand, there might be something I'm overlooking or the problem might appear deceptively trivial so it could always take longer than expected. We'll have to see.

week 6 - june 29th

This week we implemented all of the sub-cases in which the storage of the matrix in each node was traversed in a transposed manner. Unfortunately, we wrote all of this code without the ability to create matrices with these conditions to test the algorithms on. Once the ability to create such matrices is added to the pMatrix container, we will be able to confirm that these algorithms work as intended, both performance-wise and correctness.

We also wrote specializations for the last two configurations of the matrix multiplication algorithm (RRC & CCR). This brings the total amount of specializations to 8 out of 8 with all of the sub-specializations tentatively complete. The last two specializations however are very inefficient; they employ the use of a temporary matrix to store the transposed version of one of the matrices. The transposition is a simple p_copy, which in our case is incredibly slow (around 15-20 times slower). The only other solution we came up for this problem was a new algorithm that calculated p^2 multiplications as opposed to the usual amount of p multiplications.

For the next week, we should definitely work on improving the algorithm for the last two cases. This would require an efficient implementation of a parallel transpose or a totally new algorithm. We would also need to test the sub-cases with the non-native traversals, but this should take significantly less time than the former problem.

week 7 - july 6th

Over the week, we had finished testing all of the cases that a block-band matrix could be passed to our algorithm. This required tweaking and testing 64 different specialization and confirming that each case produced the correct results. Surprisingly, our algorithm passed on all of the cases. For 75% of the specializations, the execution time and speedup should be directly comparable to the algorithm that was provided to us because the only overhead introduced for those cases came at compile-time. However, we could not get any direct performance data because of the way were testing the code. Since the ability for a pMatrix to have block views whose data is traversed in a transposed manner is still not yet implemented, we created a temporary means to test our algorithm which will work in the future, should this feature be implemented in STAPL. For the other cases, the execution times were considerably worse simply due to the fact that they rely on an efficient reshape algorithm. For next week, we could possibly consider ways to improve this algorithm or implement a new reshape method.

We have also started writing our research paper that is due in a couple of weeks. We wrote the abstract and included some diagrams that explained what we have done over the summer. We were also informed that we might have to give a presentation to the other summer students as early as next Thursday, so we started working on a power point with the help of some already written templates provided by Antal. We will for next week continue working on our research paper, our presentation and hopefully start on our poster.

week 8 - july 13th

Since the summer is almost over, a lot of deadlines came up this week so Lena and I have been fairly busy. We ended up giving a ten minute PowerPoint presentation about our work to the other summer students this Thursday and a lot of time was spent coming up with the presentation itself. We also had to submit our abstract by the end of the week. I have attached a working copy of the research report that includes the abstract and parts of the introduction and background.

Matrix multiplication-wise, we were able to make our algorithm handle single precision floating point numbers in addition to doubles. We also added functionality for it to handle both single and double precision complex numbers, but with the way types are handled in STAPL, we were not able to figure out a way to test this. However, the calls to (s/d/c/z)gemm should be handled based on the types in the pMatrix so when there is better type handling in STAPL, our type specializations will work. We are also almost finished with the general case for matrix multiplication where the views are not fast views. We are currently having issues with the transposed iterator wrapper, but the people working on it are aware of this and they can come up with a fix. By next week, this should be finally implemented and our algorithm should be able to handle all cases, not just block-band partitions.

week 9 - july 20th

With this week being my second to last week at Texas A&M, I've naturally been scrambling to get everything done before the deadlines become too unbearable. Lena and I finished our poster and we are ready to present it next week. With the both the poster and presentation out of the way, we have only the research paper left. Next week will be spent frantically trying to get the paper done and presenting our poster.

Specialization-wise, we were able to finish writing a general case that accepted views of any kind and produced a result in the same way as the other algorithms (multiply and roll). It is using STL's innerproduct, so it's naturally not as fast as BLAS, but it is still scalable. We have only tested it for block views, but it should theoretically work for any view that is passed to it since it depends mostly on the data traversal of Antal's new view types. So to recap, for the nine weeks I have been here, we implemented six new algorithms with 8 specializations each to take advantage of data storage/traversal and we have just finished creating the general algorithm that works for all cases.

week 10 - july 27th

My last week at Texas A&M was incredibly exciting and extremely memorable. It consisted mostly of me scrambling to get everything turned in and completed in a reasonable amount of time while still retaining a modest sleep schedule. Final touches were made on our poster and the majority of the research paper was written. The two poster presentations went extremely well because it was the first time that I ever gave a presentation about something I actually cared about. I'm sure it showed. Although I did not win any awards, I still enjoyed myself this summer and realized that a career in research is definitely a long-term goal of mine and graduate study will be my focus in the short-term. I'd like to sincerely thank everyone involved for making this summer a memorable one.